二级通识
循环结构
循环队列
- 例题一

解析:
咱把循环队列想象成一个头尾相连的环形跑道,跑道上有一些位置能放东西。队头指针
front就像是在跑道上标记从哪儿开始取东西,队尾指针rear标记着下一个能放东西的位置。一般来说,要是队头和队尾都在跑道的最后一个位置(也就是
front = rear = m,这里m是跑道总共能放东西的位置数量 ),那就说明跑道上啥东西都没有,队列是空的。但要是队头和队尾在同一个位置,可又不是跑道最后那个位置(像这题里
front = rear = 25,不是 50 ),这时候队列可能是空的,也可能是摆满东西了。这题说又成功放进去一个东西,要是队列已经摆满了,就没地方放新东西了,所以就说明之前队列是空的。那放进去一个东西后,队列里自然就只有这 1 个东西啦,答案就是 A 选项。
例题二

关于以上公式:
当front<rear时:
在循环队列里,
front指向队头元素的前一个位置 ,这是一种约定的表示方式。这么设定主要是为了方便处理入队和出队操作时指针的移动逻辑 。我们再结合例子详细说。就像刚才那道题,
front = 24,rear = 25。- 你可以把队列想象成一排座位(这里是循环的 )。
front指向的 24 号位置,它前面没有元素(因为它是队头元素前一个位置 ) ,rear指向的 25 号位置有一个元素(队尾元素 )。 - 从元素个数角度看,我们关注的是有元素的位置数量。
rear所指位置有元素,front所指位置没有元素,那么从没有元素的front位置(24 号 )到有元素的rear位置(25 号 ),中间就只有 1 个有元素的位置,所以元素个数就是rear - front = 25 - 24 = 1。
再举个例子,如果
front = 1,rear = 3,front指向的 1 号位置没有元素,从 1 号位置到 3 号位置,中间有 2 个有元素的位置(2 号和 3 号 ),元素个数就是3 - 1 = 2。- 你可以把队列想象成一排座位(这里是循环的 )。
当front>rear时
当
front > rear时 ,我们还是以环形的视角来理解循环队列。假设循环队列存储空间为
Q(1:50),现在front = 45,rear = 5。从实际的存储角度看,队尾元素在 5 号位置,队头元素前一个位置在 45 号位置。由于是循环队列,不能简单用
rear - front计算元素个数,因为这样会得到负数。我们可以这样想:从 45 号位置开始,要数到 5 号位置有多少个元素。因为是环形,相当于从 45 号位置先走到 50 号位置,这走了
50 - 45 = 5个位置 ,然后再从 1 号位置走到 5 号位置,又走了 5 个位置,总共走的位置数就是元素个数,也就是(50 - 45)+ 5 = 10。用公式表示就是元素个数为
rear - front + m(这里m是队列存储空间大小,本题中m = 50) ,代入数值就是5 - 45 + 50 = 10。本质上,
rear - front + m这个公式是考虑到了循环队列绕圈的特性,通过加上队列总长度m,来保证能正确计算出队头和队尾之间的元素个数 。个人更喜欢公式:m-front+rear。
栈和队列
做题注意

- 这题玩文字游戏:这里说的是轮流进入/出栈,轮流进入/退队,所以逻辑是
A,C,E,G入栈,B,D,F,H入队,出栈和出队也是这个顺序。
关于栈的top指针
- 例题:

- 入栈:top指针递减1,**出栈:**top指针增加1:
- 原因:指针
top始终指向栈顶的位置,top赋值为51,意味着刚开始指针在范围之外,栈为空,一个元素入栈后,top值会减一,一直到top值为1。
数组
排序
- 排序比较数

- 记住上面的公式
程序化结构
结构化程序的基本控制结构
- 顺序,选择和重复。
数据库
关系数据库
- 关系模式是用来记录用户数据的
二维表。 
数据库模型
- 概念模型:它是对现实世界的抽象表示,不依赖于具体的计算机系统和数据库管理系统(DBMS),主要用于数据库设计阶段,帮助人们理解和分析数据以及数据之间的关系 。
- 逻辑模型:是从计算机角度对数据进行的抽象,依赖于 DBMS ,层次模型、网状模型、关系模型都属于逻辑模型 。
- 例子:
- A. 层次模型:用树形结构来表示实体及实体间联系,是早期数据库采用的模型 ,属于逻辑模型。比如在企业组织架构中,可以用层次模型表示部门和员工的上下级关系。
- B. 关系模型:以二维表格形式来组织数据,是目前应用最广泛的数据库模型 ,如常见的 MySQL 数据库就基于关系模型,属于逻辑模型。
- C. 网状模型:用网络结构表示实体及实体间联系,比层次模型更具灵活性,但结构复杂 ,也属于逻辑模型。
- D. 实体 - 联系模型(E - R 模型):通过实体、联系、属性三个要素来描述现实世界的概念模型 。例如在学校管理系统中,学生是实体,课程是实体,学生选课就是两者之间的联系,学生的姓名、学号等就是属性。所以实体 - 联系模型是概念模型 ,本题答案为 D。
范式
1NF
- 基本介绍
- 定义:关系模式中的每个属性都不可再分,即属性是原子的。并且主属性(主键)不能为空且不重复 。例如学生选课关系模式中,每个属性如 “学号”“课程号” 等都不能再拆分成更小的子属性 ,这是关系型数据库最基本要求。
- 比如:
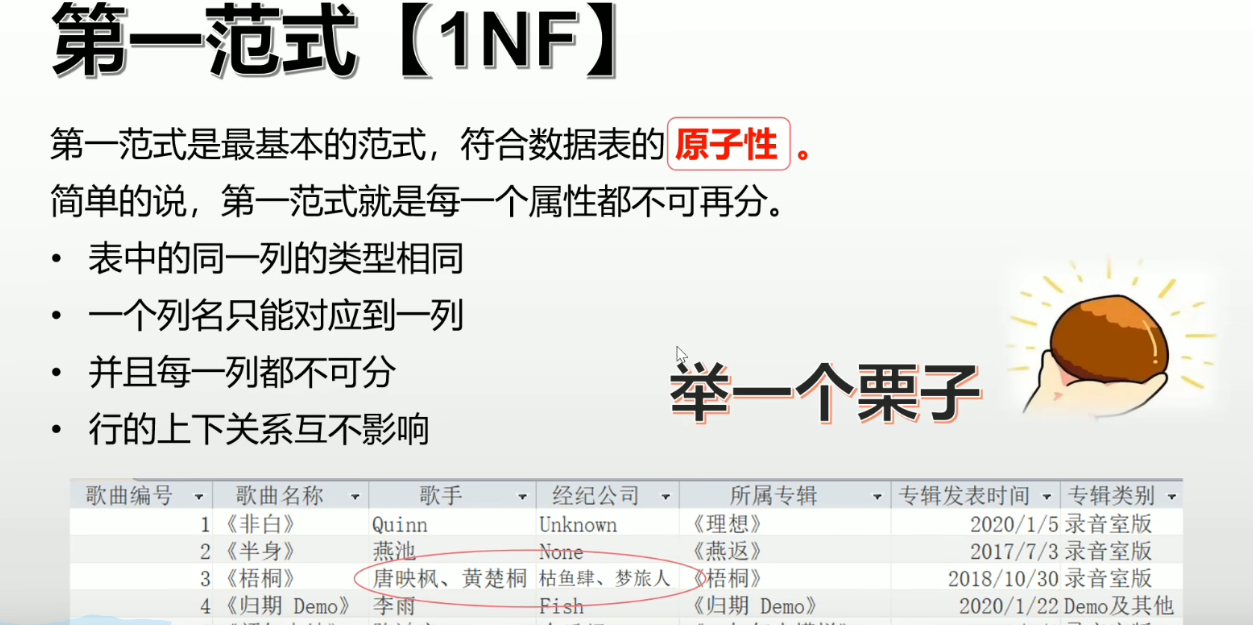
- 这里的歌手一列含有两个元素,不符合原子化的规范。比如学习成绩,这一栏就会有如:
{"英语":100,"数学":100}的情况,这一栏就不符合原子化的原则,即不为1NF的规则。
2NF
- 基本介绍
- 定义:在满足 1NF 基础上,要求关系模式中的每个非主属性完全依赖于主键,而不能只依赖于主键的一部分。
- 举个例子:
- 假设存在一个电商的 “订单信息表” ,包含属性(订单号,商品编号,商品名称,单价,购买数量,客户编号,客户姓名 )。
- 确定主键:这里(订单号,商品编号)作为主键,因为一个订单可以包含多种商品,只有两者结合才能唯一确定一条记录。
- 判断函数依赖: “商品名称”“单价” 只依赖于 “商品编号” ,“客户姓名” 只依赖于 “客户编号” 。也就是说,它们只是依赖于主键(订单号,商品编号)中的一部分属性,存在部分函数依赖。比如知道商品编号就能确定商品名称,不需要订单号参与 ,所以这个表不满足 2NF。
- 优化方案:可以将这个表拆分为 “订单表”(订单号,商品编号,购买数量,客户编号 )、“商品表”(商品编号,商品名称,单价 )、“客户表”(客户编号,客户姓名 ),这样拆分后每个表中的非主属性都完全依赖于主键,满足 2NF。
3NF
- 基本介绍
- **定义:**第三范式(3NF)要求关系模式在满足第二范式(2NF)的基础上,不存在非主属性对主键的传递函数依赖 。
- 举例:

- 相当于横向有依赖。其解决方法也是把表拆开。

- 解决方法如图所示。
BCNF
例题
例题一
- 对于这个题目,我们先判断主键是什么:
- 在关系模式
SC(S#,Sn,C#,Cn,G,Cr)中,要唯一确定一条学生选课记录,需要同时知道学生的学号(S#)和课程号(C#),所以主键是(S#,C#) 。
- 在关系模式
- 分析函数依赖关系
- 函数依赖 “
S# → Sn”(学号决定姓名) ,即知道学号就能确定学生姓名;“C# → Cn”(课程号决定课程名) ,即知道课程号就能确定课程名。 - 这里 “
Sn”(姓名)只依赖于主键中的 “S#”(学号) ,“Cn”(课程名)只依赖于主键中的 “C#”(课程号) ,存在非主属性对主键的部分函数依赖。 - 第一范式(1NF):该关系模式中每个属性(学号、姓名、课程号、课程名、成绩、学分)都是不可再分的原子值,满足 1NF。
- 第二范式(2NF):由于存在非主属性(如 “
Sn”“Cn” )对主键的部分函数依赖,不满足 2NF。 - 因为不满足 2NF,自然也不满足更高等级的 3NF 和 BCNF。
- 函数依赖 “
算法
- 算法可以用各种方式来描述,
N-S流程图把算法的每一步使用一个矩形框来表示,一个个矩形框按执行的次序来链接就是一个算法描述。 - 使用三种基本算法:顺序、循环、选择结构就可以实现任何复杂的算法。
计算机数据
计算机数据类型及其作用
原码
简单数据表示:原码的表示方式简单直观,在一些对运算要求不高,仅用于数据展示或简单存储的场景中,原码可以方便人们直观地看出数据的正负和数值大小,比如在一些数据的输入输出阶段。
特定乘法运算:原码在乘法运算中相对简便,进行乘法运算时,只需将尾数相乘,符号位单独处理 。
补码:
在计算机中,整数的存储和运算通常采用补码形式。补码可以将减法运算转化为加法运算,简化计算机硬件的设计;同时,补码表示下0的表示唯一,利于计算机的运算和处理。
反码
早期计算机系统:在早期的一些计算机系统,如PDP-1和CDC 6600中,曾使用反码来表示负数。
错误检测:在某些简单的错误检测机制,如奇偶校验中,反码可以用于快速检测数据在传输过程中是否出现错误 。
特定硬件与教学:在教学领域,反码是计算机组成原理中重要的教学内容;在一些特定的嵌入式系统或专用硬件中,反码能在某些情况下简化加减法运算(两个反码相加,若最高位产生进位,则在结果上加1 ) 。
偏移码(移码):
常用于浮点数的阶码表示。在浮点数运算中,使用移码表示阶码,能方便地对阶码进行比较和运算,同时保证浮点数的机器零为全0,便于计算机对浮点数的处理和存储 。
软件工程
测试方式
- 黑盒测试技术的依据:主要依据需求规格说明书里对软件功能的描述,强调功能
- 比如:一个计算器软件,需求规格说明书会写明它能进行加、减、乘、除等运算。黑盒测试就根据这些功能描述,去验证输入不同数字和运算符号组合时,软件是否能正确输出结果 ,而不考虑计算器内部代码是如何实现这些运算的。
- 白盒测试的技术依据:依据软件设计说明书、程序内部逻辑结构进行测试,强调内部逻辑
- 比如:开发一个电商系统,在单元测试时用白盒测试检查每个商品模块的功能代码
软件的生存周期
- A. 可行性研究:判断软件项目是否值得做、能否做。如开发在线教育软件,评估技术上能否实现直播授课,经济上投入产出是否合理
- B. 需求分析:确定软件要做什么。如在线教育软件,明确要实现课程播放、作业布置、考试测评等功能 。
- C. 软件设计:规划软件怎么做。如在线教育软件,设计课程播放模块架构、数据库表结构等 。
- D. 软件实现:用代码实现软件功能。如在线教育软件,编写代码实现课程播放、用户登录等功能 。





